Sistemas Numéricos

 

Os sistemas de numeração dividem-se em dois grandes grupos: sistemas numéricos posicionais e não-posicionais.

 

o valor atribuído ao símbolo depende da posição que ele ocupa em relação ao conjunto.

Exemplo:

			777 =   700    +    70   +    7

No exemplo dado, o símbolo 7 da posição mais à esquerda vale 700, o da posição intermediária, vale 70 e o da direita, 7. Ou seja ao mudar o simbolo de posicao seu valor é alterado.

os símbolos possuem valores definidos e imutáveis, não dependendo da posição que ocupam no conjunto de que fazem parte.

Exemplo:

				X	= 10
				XI	= 10 + 1
				XII	= 10 + 1 + 1

O símbolo X encontrado nos três conjuntos acima tem um valor constante (10), embora ele tenha variado de posição em cada conjunto. No primeiro conjunto, o algarismo romano X ocupa a primeira e única posição; no segundo, ele ocupa a segunda posição, a contar da direita para a esquerda; e no terceiro conjunto, ocupa a posição de número três. Como se vê, o algarismo muda de posição, mas seu valor continua imutável. Portanto, não depende de sua posição em relação ao conjunto.

 

Uma base numérica representa a quantidade de algarismo ou símbolos que podem ser usados para a representação de um sistema numérico. As bases numéricas mais conhecidas são:

Este sistema consiste em um conjunto dez símbolos que vão de 0 até 9 (0, 1, 2, 3, ..., 9), isso permite representar o valor dos números em unidades individuais, mas para representar um valor maior que nove é necessário combina-los.

A regra para associar os números às respectivas quantidades é simples: Comece com o algarismo zero. Utilize os demais dígitos para os próximos nove números. Uma vez que o dígito na posição corrente atinge 9, pulamos para a esquerda dessa posição e atribuímos o algarismo 1 e retomamos a posição anterior a partir do algarismo 0 repetindo a contagem:

00, 01, 02, ... 07, 08, 09 (o dígito à direita reinicia, e o à esquerda passa de 0 para 1)
10, 11, 12, ... 17, 18, 19 (o dígito à direita reinicia, e o à esquerda passa de 1 para 2)
20, 21, 22, ...

No sistema binário, temos apenas dois algarismos (0 e 1) para compor números. A regra continua a mesma da utilizada para os números decimais. Começamos com o algarismo 0 e para o próximo número, utilizamos o 1. O dígito à esquerda avança para o próximo símbolo (0 ou 1) e a contagem à direita retorna para o símbolo 0:

000, 001
010, 011
100, 101
110, 111...

Nesse sistema, números são representados com oito algarismos (0, 1, 2, 3, 4, 5, 6 e 7). A contagem acontece da seguinte forma:

00, 01, 02, 03, 04, 05, 06, 07 ,
10, 11, 12, 13, 14, 15, 16, 17,
20, 21, …

No sistema hexadecimal, representamos números com dezesseis símbolos, que vão de 0 até 9 seguido das letras A até F (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E e F), onde as letras são equivalentes no sistema decimal aos valores de 10 até 15. Assim sua contagem será:

00, 01, 02, 03, 04, 05, 06, 07, 08, 09, 0A, 0B, 0C, 0D, 0E, 0F,
10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F,
20, 21, 22, ...

Com intuito de apoiar o aprendizado sobre os Sistemas posicionais e não-posicionais, sugere-se assistir a videoaula para o aperfeiçoamento no conhecimento deste conteúdo.

 

Observe o conjunto de algarismo 110. Qual é a quantidade que ele representa? Isto depende de qual base numérica estamos utilizando. Sem essa informação adicional, 110 é um dado que pode ser interpretado de diferentes maneiras, dependendo do sistema numérico (decimal, binário, octal, hexadecimal).

Por este motivo, para evitar diversas interpretações, usa-se a seguinte convenção: números no sistema decimal são representados na forma convencional. Nos demais casos, as bases são indicadas como um subscrito ao lado do número. Por exemplo: 110, 110₂, 110₈ ou 110₁₆

Para fazermos a conversão de qualquer base numérica para a base decimal usamos a noção de notação posicional, vista anteriormente. Pegamos o número que queremos converter e separamos seus algarismos de acordo com suas posições, então multiplicamos esses algarismos pela sua base correspondente elevada a sua posição (começando pela posição 0). E por fim somamos todos os valores, de acordo com a seguinte formula:

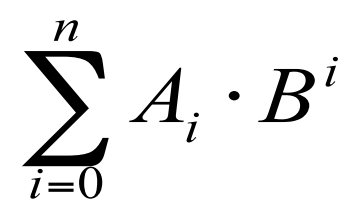
Em que A é o algarismo que ocupa determinada posição, B é a Base a qual o número pertence e i é a posição do algarismo.

Exemplo 1:

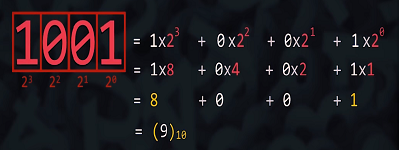
Exemplo 2:

Atente-se no exemplo acima que o símbolo C corresponde ao valor 12 do Sistema Decimal..

Com intuito de apoiar o aprendizado sobre conversões para a base Decimal, sugere-se assistir a videoaula para o aperfeiçoamento no conhecimento deste conteúdo.

 

O método para converter um número decimal para outra Base consiste em Efetuar divisões inteiras sucessivas pela base de destino até zerar o quociente. O resultado final da conversão é formado pelos restos das divisões, tomados a partir do último resto para o primeiro.

Exemplo :

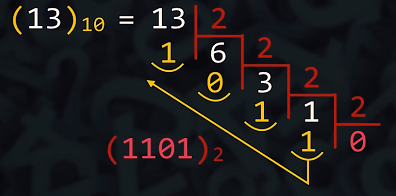
Observe no exemplo a conversão do valor 13 da base decimal, para a base binaria(2). Por meio de diversas divisões inteiras até obter o resto igual a zero, sendo assim valor correspondente encontrado é 1101.

Exemplo :

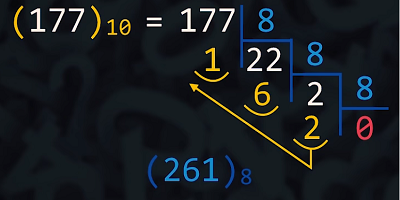
Conforme observamos no exemplo acima que exemplifica a conversão do número decimal 177 para seu correspondente em octal (261), o método utilizado segue o mesmo padrão para as outras bases.

Para realizar uma conversão de octal para binário, primeiro precisamos saber que 1 algarismos da base octal corresponde a 3 da base Binária, sendo o contrário também valido. Ou seja 3 algarismos binários correspondem a 1 Octal. Observe o exemplo abaixo:

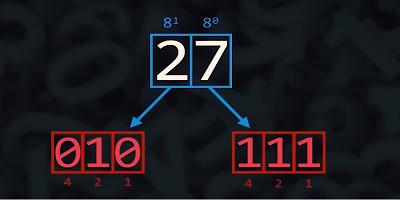
Após separados os algarismos, sua conversão e feita de maneira similar ao Decimal e por fim os resultados individuais são reunidos, então o valor Binário correspondente ao exemplo é: 10111₂.

O caminho contrário para a conversão de binário para Octal é muito similar, separa-se o número binário em conjuntos de 3 algarismos e em seguida realiza a conversão individualmente nesses conjuntos, igual a conversão decimal. Conforme a imagem:

Após realizada as conversões dos conjuntos de números binários os valores obtidos são reunidos, formando um número em Octal, assim no exemplo acima o resultado seria: 105₈

O método para realizar as conversões entre números hexadecimais e binários é muito similar as conversões Octal/Binário, a diferença está somente na relação, em que uma quádrupla(4) de dígitos Binários forma um dígito Hexadecimal, enquanto que na octal, são necessários apenas três dígitos.

Exemplo :

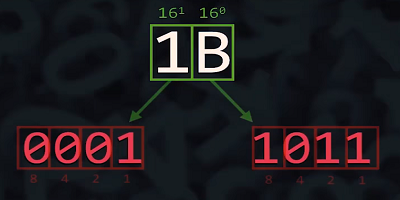
Após fazer as conversões dos conjuntos da mesma forma que a é feita para o sistema decimal, lembrando que no sistema hexadecimal o símbolo B equivale ao valor 11 na base decimal. Resta apenas fazer a junção dos valores obtendo como resultado: 11011₂ (zeros a esquerda são desconsiderados).

Já para fazer a relação contraria o número binário deve ser separado em grupos de quatro algarismos, realizando as devidas conversões para o sistema decimal, como mostrado nos exemplos anteriores também exemplificado a seguir:

Observe na imagem anterior em que o valor binário 1011101₂ é dividido em 2 grupos de quatro elementos, 0101 e 1101, que na base Decimal equivalem respectivamente a 5 e 13. Lembrando sempre que o valor 13 é representado pela letra D, sendo assim o valor final seria: 5D₁₆

Com intuito de apoiar o aprendizado sobre conversões entre bases Binaria, Octal e Hexadecimal, sugere-se assistir a videoaula para o aperfeiçoamento no conhecimento deste conteúdo.

     

No intuito de fixar a aprendizagem iniciada por meio deste módulo e verificar como seu entendimento sobre este conteúdo está, estão sendo sugeridos alguns exercícios de fixação para serem resolvidos. Clique no link de exercícios ao lado, pois será por meio dele iniciada a lista de exercícios sobre os conteúdos estudados até este momento nesta disciplina.